Google and Yahoo creating Brain Drain?
Revenge of the Nerds - Again
BusinessWeek articleSlashdot Discussion
Quaternion Multiplication
Q1 = [s1,(x1,y1,z1)]
Q2 = [s2,(x2,y2,z2)]
Q = Q1 * Q2 = [s,(x,y,z)]
s = s1*s2 - x1*x2 - y1*y2 - z1*z2;
x = s1*x2 + s2*x1 + y1*z2 - y2*z1
y = s1*y2 + s2*y1 + z1*x2 - z2*x1
z = s1*z2 + s2*z1 + x1*y2 - x2*y1
Firefox downloads reach 75 million
Slashdot Article
Essential Maths for Computer Graphics (EMCG) - 1

Playing the Trump Card
- by Christopher Howard
Einstein once said, "We can't solve a problem at the same level of thinking we used to create the problem." Relative to business, if we want to move past financial barriers and increase our own ability to make monëy, we've got to explore new ways of thinking and behaving beyond our normal parameters. In other words, sometimes going out of our minds is a good thing, especially when we can get into someone else's head like billionaire genius Donald Trump.
Business Profile:
Son of a contractor, six billion dollar net worth, nearly half the New York skyline and seven new skyscrapers going up in his name, four golf courses, three best-selling books, the number one top rated reality show "The Apprentice" and a soon-to-be-released Trump credït card. Even with his casinos $1.8 billion in dëbt, Trump is seemingly invincible.
How has one man been able to achieve so much? What values and assumptions drive him? What traits, attitudes and strategies set him apart from all the average wage earners and business owners out there? And more importantly, how can you begin to adopt these strategies yourself to propel yourself on to massive success? Let's break down just a small portion of the mindset that has allowed Donald Trump to create all that he has.
Formula for Success:
If Trump were to give us his own success formula it might be Efficiency + Discipline = Power, power being the ability to act effectively to get things done. Trump starts each day by waking up at 6 a.m. to read several newspapers in order to keep on top of what's going on in the world. He doesn't leave the office until at least 6: 30 p.m. every day. Although he works long hours he maintains the attitude that it's not how many hours you put in, it's what you get done that's important. As he puts it in
The Art of the Deal, "You consistently do the things that you know will get
results. You push forward, then you push forward some more, and you nevër let your adversaries see you worried."
Trump himself also credïts toughness as the secrët to his survival. Throughout his schooling in a military academy, Trump respected a teacher by the name of Theodore Dobias, a former Marine drill sergeant who would slap him around if he spoke back to him. Till this day, Trump will fight when he feels he's up against a wall, even when it's financially risky. He even cultivates this tough image, knowing that the other side "won't even bother asking for certain things when they think you are invincible."
Personality Profile:
Those are some of the strategies and character traits that have made the man. Herë are a few values and beliefs you can try on for size: Trump has been quoted as saying, "Monëy in itself is not a very interesting commodity. What is fascinating, to me at least, is the game we all play.
If you have a striving personality, the challenge matters most, not the reward." He put his monëy (and the city's monëy) where his mouth is on his proposed deal to renovate New York's crumbling Commodore Hotel. Where everyone else saw a lost cause, Trump saw potential and boldly asked the city for an unprecedented forty year tax abatement to turn it around.
As an overall strategy, Trump shoots for the moon and keeps pushing until he gets the moon. His success today is essentially built on that bit of bravado.
It's also become a Trump hallmark to be the best and out-shine the rest.
After New York spent six years trying unsuccessfully to re-build Central Park's ice-skating rink, Trump stepped in completing it in less time for less monëy. He did it by choosing a Canadian contractor because, "Ice skating is to Canadians what baseball is to Americans - the national pastime." In fact, Trump values quality so highly he is notorious for hiring the most-qualified people from his competitors and out-paying them.
If you're going to think at all, you might as well think big when learning from the super successful, pick and choose which aspects of the billionaire's mindset serve your own values and your company's mission. Expanding your perspective will expand your choices and therefore your horizons. This week, see how you would run your business differently if you tried on Trump's shoes for size. How would you make decisions if you looked at life as a game and monëy as the means for keeping score? What bïgger challenges might you take on for greater rewards? When problem-solving consider, "What would 'The Donald' do?" Be able to recognize valuable opportunïties where others see crumbling lost causes.
And next time you go into negotiations, play your Trump card and see how it can pay off in spades.
Multithreaded programs in C++
A Link
Standard Template Library Programmer's Guide
http://www.sgi.com/tech/stl/
DPS

Sweet Memories....
GUI Software Using C++
#include
#include
#include
#include
#include
#include
#include
/*MOUSE VARIABLES */
union REGS in,ou;
int but,xm,ym;
int mx,my;
/*TEMPORARY VARIABLES*/
int mtmp=0;
int cmenut=10;
int menut=0;
initmouse();
void showmouseptr();
void hidemouseptr();
void restrictmouseptr(int,int,int,int);
void getmousepos();
void *timage;
/*BUTTON CLASS*/
class button
{
/*X1,Y1,X2,Y2 - BUTTON CO-ORDINATES
UP,MI,DOW - BUTTON COLORS
DEP - BUTTON DEPTH
CAP - CAPTION*/
int x1,y1,x2,y2,up,mi,dow,dep,ptmp;
char cap[100];
public:
/*BUTTON CONSTRUCTORS WHICH DRAWS BUTTON*/
button (int x1,int y1,int x2,int y2,int up,int mi,int
dow,int dep,char *cap)
{
this->x1=x1;
this->y1=y1;
this->x2=x2;
this->y2=y2;
strcpy(this->cap,cap);
this->dep=dep;
this->up=up;
this->dow=dow;
this->mi=mi;
ptmp=0;
setlinestyle(0,0,0);
setfillstyle(1,mi);
bar (x1,y1,x2,y2);
setcolor (dow);
line (x2,y1,x2+dep,y1-dep);
line (x2+dep,y1-dep,x2+dep,y2+dep);
line (x2+dep,y2+dep,x1-dep,y2+dep);
line (x1-dep,y2+dep,x1,y2);
line (x1,y2,x2,y2);
line (x2,y2,x2,y1);
setfillstyle(1,dow);
floodfill (x2-dep,y2+dep-1,dow);
setcolor (up);
line (x1-dep,y1-dep,x2+dep,y1-dep);
line (x2+dep,y1-dep,x2,y1);
line (x2,y1,x1,y1);
line (x1,y1,x1,y2);
line (x1,y2,x1-dep,y2+dep);
line (x1-dep,y2+dep,x1-dep,y1-dep);
setfillstyle(1,up);
floodfill (x1,y1-dep+1,up);
setlinestyle(3,3,3);
/*CLOSE, MAXIMIZE, MINIMAZE BUTTONS*/
if (strcmp("CLO",cap)==0)
{
setcolor(0);
setlinestyle(0,0,3);
line(625,10,630,15);
line(625,15,630,10);
}
else if (strcmp("MAX",cap)==0)
{
setcolor(0);
setlinestyle(0,0,2);
rectangle(611,9,618,16);
rectangle(611,10,618,15);
}
else if (strcmp("MIN",cap)==0)
{
setcolor(0);
setlinestyle(0,0,2);
rectangle(598,15,604,16);
}
else
{
settextjustify(CENTER_TEXT,CENTER_TEXT);
setcolor(0);
outtextxy((x1+x2)/2,(y1+y2)/2,cap);
settextjustify(LEFT_TEXT,RIGHT_TEXT);
}
}
/*FUNCTION WHICH CHECKS WHETHER THE BUTTON IS PRESSED
OR NOT. IF PRESSED, RETURNS 1*/
int pressed()
{
getmousepos();
if (xm>x1&&xmy1&&ym {
if (ptmp==0)
{
hidemouseptr();
mtmp=1;
press(dow,mi,up);
ptmp=1;
showmouseptr();
}
return 0;
}
else if (ptmp==1&&but==0)
{
hidemouseptr();
ptmp=0;
press(up,mi,dow);
showmouseptr();
return 1;
}
else return 0;
}
/*FUNCTION WHICH GENERATES PRESS EFFECT OF THE
BUTTON*/
void press(int up,int mi,int dow)
{
setlinestyle(0,0,0);
setfillstyle(1,mi);
bar (x1,y1,x2,y2);
setcolor (dow);
line (x2,y1,x2+dep,y1-dep);
line (x2+dep,y1-dep,x2+dep,y2+dep);
line (x2+dep,y2+dep,x1-dep,y2+dep);
line (x1-dep,y2+dep,x1,y2);
line (x1,y2,x2,y2);
line (x2,y2,x2,y1);
setfillstyle(1,dow);
floodfill (x2-dep,y2+dep-1,dow);
setcolor (up);
line (x1-dep,y1-dep,x2+dep,y1-dep);
line (x2+dep,y1-dep,x2,y1);
line (x2,y1,x1,y1);
line (x1,y1,x1,y2);
line (x1,y2,x1-dep,y2+dep);
line (x1-dep,y2+dep,x1-dep,y1-dep);
setfillstyle(1,up);
floodfill (x1,y1-dep+1,up);
setlinestyle(3,3,3);
/*IF CLOSE BUTTON*/
if (strcmp("CLO",cap)==0)
{
setcolor(0);
setlinestyle(0,0,3);
line(625,10,630,15);
line(625,15,630,10);
}
/*IF MAXIMIZE BUTTON*/
else if (strcmp("MAX",cap)==0)
{
setcolor(0);
setlinestyle(0,0,2);
rectangle(611,9,618,16);
rectangle(611,10,618,15);
}
/*IF MINIMIZE BUTTON*/
else if (strcmp("MIN",cap)==0)
{
setcolor(0);
setlinestyle(0,0,2);
rectangle(598,15,604,16);
}
else
{
settextjustify(CENTER_TEXT,CENTER_TEXT);
setcolor(0);
outtextxy((x1+x2)/2,(y1+y2)/2,cap);
settextjustify(LEFT_TEXT,RIGHT_TEXT);
}
}
};
button *butall;
/*CHKBOX CLASS*/
class checkbox
{
public:
/*X,Y - CO-ORDINATES
CAP - CAPTION*/
int x,y,chk;
char cap[100];
/*CHECKBOX CONSTRUCTOR WHICH DRAWS CHECKBOX */
checkbox(int x,int y,char *cap)
{
chk=0;
this->x=x;
this->y=y;
strcpy(this->cap,cap);
butall=new button(x,y,x+9,y+9,8,15,7,1,"");
setcolor(8);
setlinestyle(0,0,0);
rectangle(x,y,x+10,y+10);
settextstyle(SMALL_FONT,HORIZ_DIR,4);
settextjustify(LEFT_TEXT,CENTER_TEXT);
setcolor(0);
outtextxy(x+20,y+3,cap);
}
/*FUNCTION TO CHECK/UNCHECK THE CHECKBOX*/
int pressed()
{
getmousepos();
if
(xm>x-2&&xmy-2&&ym {
hidemouseptr();
setlinestyle(0,0,0);
setcolor(0);
line (x-1,y+1,x-3,y+3);
line(x-1,y+1,x+3,y+9);
line(x+3,y+9,x+15,y-1);
line (x-1,y-1,x-3,y+3);
line(x-1,y-1,x+4,y+5);
line(x+4,y+5,x+15,y-1);
line (x-1,y-1,x-3,y+3);
line(x-1,y-1,x+4,y+6);
line(x+4,y+6,x+15,y-1);
line(x-1,y-1,x+4,y+7);
line(x+4,y+7,x+15,y-1);
line(x-1,y-1,x+4,y+8);
line(x+4,y+8,x+15,y-1);
showmouseptr();
chk=1;
mtmp=1;
return 1;
}
else if
(xm>x-2&&xmy-2&&ym {
hidemouseptr();
butall=new button(x-4,y-2,x+15,y+12,7,7,7,0,"");
chk=0;
mtmp=1;
draw();
showmouseptr();
return 1;
}
else return 0;
}
/*DRAWS THE CHECKBOX*/
void draw()
{
butall=new button(x,y,x+9,y+9,8,15,7,1,"");
setcolor(8);
setlinestyle(0,0,0);
rectangle(x,y,x+10,y+10);
}
/*CHECKS THE CHECKBOX*/
void check()
{
setcolor(0);
line (x-1,y+1,x-3,y+3);
line(x-1,y+1,x+3,y+9);
line(x+3,y+9,x+15,y-1);
line (x-1,y-1,x-3,y+3);
line(x-1,y-1,x+4,y+5);
line(x+4,y+5,x+15,y-1);
line (x-1,y-1,x-3,y+3);
line(x-1,y-1,x+4,y+6);
line(x+4,y+6,x+15,y-1);
line(x-1,y-1,x+4,y+7);
line(x+4,y+7,x+15,y-1);
line(x-1,y-1,x+4,y+8);
line(x+4,y+8,x+15,y-1);
chk=1;
}
/*UNCHECKS THE CHECKBOX*/
void uncheck()
{
butall=new button(x-4,y-2,x+15,y+12,7,7,7,0,"");
chk=0;
draw();
}
};
/*TEXTBOX CLASS*/
class textbox
{
public :
/*X1,Y1,X2,Y2 - CO-ORDINATES
FSIZE - FONT SIZE
FONT - FONT NAME
TEXT - TEXT CONTENTS*/
int x1,y1,x2,y2,fsize,font;
char text[100];
/*CONSTRUCTOR WHICH DRAWS TEXTBOX*/
textbox(int x1,int y1,int x2,int y2,char
text[100],int font,int fsize)
{
this->x1=x1;
this->y1=y1;
this->x2=x2;
this->y2=y2;
this->fsize=fsize;
strcpy(this->text,text);
this->font,font;
draw();
settextstyle(font,HORIZ_DIR,fsize);
settextjustify(LEFT_TEXT,CENTER_TEXT);
setcolor(0);
outtextxy(x1+5,y1+6,text);
}
int pressed();
/*TEXTBOX DRAW PROCEDURE*/
void draw()
{
butall=new button(x1,y1,x2,y2,8,15,7,1,"");
setcolor(8);
setlinestyle(0,0,0);
rectangle(x1,y1,x2+1,y2+1);
}
/*SETTEXT METHOD*/
void settext(char text[100])
{
draw();
settextjustify(LEFT_TEXT,CENTER_TEXT);
setcolor(0);
outtextxy(x1+5,y1+6,text);
}
};
/*CLASS WINDOW - INTEGRATION */
class windo
{
public:
button *butwin;
button *buttitl;
button *butclo;
button *butmax;
button *butmin;
button *menubar;
windo(char *T)
{
butwin=new button(5,5,635,475,15,7,8,0,"");
buttitl=new button(5,5,636,20,9,1,0,0,"");
butclo=new button(622,7,633,18,15,7,8,0,"CLO");
butmax=new button(609,7,620,18,15,7,8,0,"MAX");
butmin=new button(596,7,607,18,15,7,8,0,"MIN");
menubar=new button(5,40,635,41,15,7,8,0,"");
menubar=new button(5,42,635,43,15,7,8,0,"");
setcolor(9);
outtextxy(16,11,T);
setcolor(15);
outtextxy(15,10,T);
settextstyle(SMALL_FONT,HORIZ_DIR,4);
}
};
/*PRESSED FUNCTION OF TEXTBOX */
int textbox::pressed()
{
/*CHECK THE EXTREMITIES*/
if (xm>x1&&xmy1&&ym {
hidemouseptr();
char txt;
char txtt[20];
int xp=x1+5;
draw();
settextjustify(LEFT_TEXT,CENTER_TEXT);
strcpy(text,"");
do
{
setcolor(0);
line (xp,y2-4,xp+3,y2-4);
txt=getch();
/*IF TEXTBOX FULL*/
if (xp>x2-6&&txt!=char(8))
{
sound(150);
delay(50);
nosound();
}
else
{
if (txt==char(8))
{
/*IF TEXTBOX EMPTY*/
if (strcmp(text,"")==0)
{
sound(150);
delay(50);
nosound();
}
else
{
text[strlen(text)-1]='\0';
xp=xp-6;
setfillstyle(1,15);
bar(xp-2,y1+2,x2-2,y2-2);
line (xp,y2-4,xp+3,y2-4);
outtextxy(x1+5,y1+6,text);
}
}
else
{
setcolor(15);
line (xp,y2-4,xp+3,y2-4);
setcolor(0);
sprintf(txtt,"%c",txt);
settextjustify(LEFT_TEXT,CENTER_TEXT);
strcat(text,txtt);
outtextxy(x1+5,y1+6,text);
xp=xp+6;
}
}
}
while(txt!=char(13));
setcolor(15);
line (xp,y2-4,xp+3,y2-4);
showmouseptr();
return 1;
}
else return 0;
}
void main()
{
/*GRAPHICS INITIALIZATION*/
int gdriver=VGA,gm=VGAHI;
char kstroke;
initgraph(&gdriver,&gm,"C:\\tc\\bgi");
windo gui("GUI THROUGH C++
(dytrivedi@rediffmail.com)");
/*CALCULATOR SECTION -- INTEGERS ONLY*/
textbox n1(50,75,90,90,"0",SMALL_FONT,4);
textbox n2(150,75,190,90,"0",SMALL_FONT,4);
textbox ans(80,185,160,200,"0",SMALL_FONT,4);
button butplus(25,125,50,150,15,7,8,0,"+");
button butminus(75,125,100,150,15,7,8,0,"-");
button butmul(125,125,150,150,15,7,8,0,"*");
button butdiv(175,125,200,150,15,7,8,0,"/");
/*STRING MANIPULATION SECTION*/
textbox s1(260,75,450,90,"",SMALL_FONT,4);
textbox s2(260,185,450,200,"",SMALL_FONT,4);
button butrev(330,125,380,150,15,7,8,0,"Reverse");
/*CHECKBOXES SECTION*/
checkbox c1(500,75,"New");
checkbox c2(500,125,"York");
textbox result(500,185,600,200,"",SMALL_FONT,4);
button butexit(550,425,600,455,15,7,8,0,"Exit");
/*SEPERATORS*/
butall = new button(230,50,231,250,15,7,8,0,"");
butall = new button(475,50,476,250,15,7,8,0,"");
butall = new button(10,260,630,261,15,7,8,0,"");
/*MOUSE INITIALIZATION AND RESTRICTION*/
if (initmouse()==0)
{
cout<<"NO MOUSE ... ";
closegraph();
exit(0);
}
restrictmouseptr(5,5,635,475);
showmouseptr();
/*THE MAIN LOOP*/
mainloop:
while(!kbhit())
{
/*GET MOUSE POSITION CONSTANTLY*/
getmousepos();
if (but==0) mtmp=0;
/*CHECKING OF EVENTS*/
/*IF CLOSE BUTTON PRESSED*/
if (gui.butclo->pressed()==1)
{
cleardevice();
closegraph();
exit(0);
}
/*IF PLUS BUTTON PRESSED*/
if (butplus.pressed()==1)
{
long int no1,no2;
char answer[10];
no1=atol(n1.text);
no2=atol(n2.text);
ltoa(no1+no2,answer,10);
ans.settext(answer);
}
/*IF MINUS BUTTON PRESSED*/
if (butminus.pressed()==1)
{
long int no1,no2;
char answer[10];
no1=atol(n1.text);
no2=atol(n2.text);
ltoa(no1-no2,answer,10);
ans.settext(answer);
}
/*IF MULTIPLICATION BUTTON PRESSED*/
if (butmul.pressed()==1)
{
long int no1,no2;
char answer[10];
no1=atol(n1.text);
no2=atol(n2.text);
ltoa(no1*no2,answer,10);
ans.settext(answer);
}
/*IF DIVISION BUTTON PRESSED*/
if (butdiv.pressed()==1)
{
float no1,no2;
char answer[10];
no1=atoi(n1.text);
no2=atoi(n2.text);
if (no2==0)
{
ans.settext("Error");
}
else
{
itoa(no1/no2,answer,10);
ans.settext(answer);
}
}
/*IF REVERSE BUTTON PRESSED*/
if (butrev.pressed()==1)
{
s2.settext(strrev(s1.text));
}
/*IF EXIT BUTTON PRESSED*/
if (butexit.pressed()==1)
{
cleardevice();
closegraph();
exit(0);
}
/*IF FIRST CHECKBOX PRESSED*/
if (c1.pressed()==1)
{
char tmp[20]="";
if (c1.chk==1)
{
strcat(tmp,c1.cap);
}
if (c2.chk==1)
{
strcat(tmp,c2.cap);
}
result.settext(tmp);
}
/*IF SECOND CHECKBOX PRESSED*/
if (c2.pressed()==1)
{
char tmp[20]="";
if (c1.chk==1)
{
strcat(tmp,c1.cap);
}
if (c2.chk==1)
{
strcat(tmp,c2.cap);
}
result.settext(tmp);
}
/*INCLUDE TEXTBOXES HERE IN ORDER TO SET THEM
WORKING*/
if (n1.pressed()==1)
{
}
if (n2.pressed()==1)
{
}
if (s1.pressed()==1)
{
}
}
/*IF NOT PRESSED ESC THEN GO TO MAIN LOOP*/
char a=getch();
if (a!=char(27)) goto mainloop;
closegraph();
}
/*MOUSE FUNCTIONS*/
initmouse()
{
in.x.ax=0;
int86 (0x33,&in,&ou);
return(ou.x.ax);
}
/*MOUSE POINTER SHOW PROCEDURE*/
void showmouseptr()
{
in.x.ax=1;
int86(0x33,&in,&ou);
}
/*MOUSE POINTER HIDE PROCEDURE*/
void hidemouseptr()
{
in.x.ax=2;
int86(0x33,&in,&ou);
}
/*FUNCTION TO RESTRICT MOUSE POINTER*/
void restrictmouseptr(int x1,int y1,int x2,int y2)
{
in.x.ax=7;
in.x.cx=x1;
in.x.dx=x2;
int86(0x33,&in,&ou);
in.x.ax=8;
in.x.cx=y1;
in.x.dx=y2;
int86(0x33,&in,&ou);
}
/*FUNCTION TO GET MOUSE POSITION*/
void getmousepos()
{
in.x.ax=3;
int86(0x33,&in,&ou);
but=ou.x.bx;
xm=ou.x.cx;
ym=ou.x.dx;
}
questions...
Assuming that i extract only a single slice, what is the slice thickness?
If i need to use 3D textures, i should have a value for z...
How should i read in the data for the slice...from the data file (i.e. colon_001s_8bit.slc) ?
Conversion to voxel coordinates
The dimensions of the volume is 512*512*361
The cast_ray_for_one_pixel() in vr.cpp has commands to convert a point to the voxel coordinates.
C_FPosition point, local;
int voxel_x,voxel_y,voxel_z;
local.x=point.x*scale.x();
local.y=point.y*scale.y();
local.z=point.z*scale.z();
voxel_x = int(local.x);
voxel_y = int(local.y);
voxel_z = int (local.z);
voxel_x, voxel_y and voxel_z are presumably the voxel coordinates.
scale.x() = 1.422
scale.y() = 1.422
scale.z() = 1.0
So for the four points we have
ll2.x=ll.x*scale.x(); ll2.y=ll.y*scale.y();ll2.z=ll.z*scale.z();
vll.x=int(ll2.x);vll.y=int(ll2.y);vll.z=int(ll2.z);
ul2.x=ul.x*scale.x(); ul2.y=ul.y*scale.y();ul2.z=ul.z*scale.z();
vul.x=int(ul2.x);vul.y=int(ul2.y);vul.z=int(ul2.z);
ur2.x=ur.x*scale.x(); ur2.y=ur.y*scale.y();ur2.z=ur.z*scale.z();
vur.x=int(ur2.x);vur.y=int(ur2.y);vur.z=int(ur2.z);
lr2.x=lr.x*scale.x(); lr2.y=lr.y*scale.y();lr2.z=lr.z*scale.z();
vlr.x=int(lr2.x);vlr.y=int(lr2.y);vlr.z=int(lr2.z);
Forming 4 corners
First arbitrarily take the edge length of the plane to be 100 world space units.
The plane lies at a distance of 1 unit from the camera position , along the positive z-direction of the camera coordinate system.
The four corners will be :
ll.x=view_origin.x + itself->view->c_sys.z_axis.x - 50.0*itself->view->c_sys.x_axis.x - 50.0*itself->view->c_sys.y_axis.x;
ll.y= view_origin.y + itself->view->c_sys.z_axis.y - 50.0*itself->view->c_sys.x_axis.y - 50.0*itself->view->c_sys.y_axis.y;
ll.z=view_origin.z + itself->view->c_sys.z_axis.z - 50.0*itself->view->c_sys.x_axis.z - 50.0*itself->view->c_sys.y_axis.z;
ul.x=view_origin.x + itself->view->c_sys.z_axis.x - 50.0*itself->view->c_sys.x_axis.x + 50.0*itself->view->c_sys.y_axis.x;
ul.y=view_origin.y + itself->view->c_sys.z_axis.y - 50.0*itself->view->c_sys.x_axis.y + 50.0*itself->view->c_sys.y_axis.y;
ul.z=view_origin.z + itself->view->c_sys.z_axis.z - 50.0*itself->view->c_sys.x_axis.z + 50.0*itself->view->c_sys.y_axis.z;
ur.x=view_origin.x + itself->view->c_sys.z_axis.x + 50.0*itself->view->c_sys.x_axis.x + 50.0*itself->view->c_sys.y_axis.x;
ur.y=view_origin.y + itself->view->c_sys.z_axis.y + 50.0*itself->view->c_sys.x_axis.y - 50.0*itself->view->c_sys.y_axis.y;
ur.z=view_origin.z + itself->view->c_sys.z_axis.z + 50.0*itself->view->c_sys.x_axis.z + 50.0*itself->view->c_sys.y_axis.z;
lr.x=view_origin.x + itself->view->c_sys.z_axis.x + 50.0*itself->view->c_sys.x_axis.x - 50.0*itself->view->c_sys.y_axis.x;
lr.y=view_origin.y + itself->view->c_sys.z_axis.y + 50.0*itself->view->c_sys.x_axis.y - 50.0*itself->view->c_sys.y_axis.y;
lr.z=view_origin.z + itself->view->c_sys.z_axis.z + 50.0*itself->view->c_sys.x_axis.z - 50.0*itself->view->c_sys.y_axis.z;
Slice View
- Form the 4 corners of the plane perpendicular to the current view direction
- Convert the corners to volume space i.e. find the voxel coordinates
- Store the voxel coordinates in 3D texture
Vision
Cognex
Ensco
Image Sensing Systems
Coreco
Evolution Robotics
Advanced Interfaces
Questec
Inspeck
Vividgroup
Study to measure the power of prayer
With government funding, researchers will try to determine if 'distant healing' can help make patients well
Saturday, July 16, 2005
By HILARY E. MACGREGOR
LOS ANGELES TIMES NEWS SERVICE
SAN FRANCISCO -- On an operating table at a medical center in San Francisco, a breast cancer patient is undergoing reconstructive surgery after a mastectomy. But this will be no ordinary surgery. Three thousand miles away, a shamanic healer has been sent the woman's name, a photo and details about the surgery.
For each of the next eight days, the healer will pray 20 minutes for the cancer patient's recovery, without the woman's knowledge. A surgeon has inserted two small fabric tubes into the woman's groin to enable researchers to measure how fast she heals.
The woman is a patient in an extraordinary government-funded study that is seeking to determine whether prayer has the power to heal patients from afar -- a field known as "distant healing."
While that term is probably unfamiliar to most Americans, the idea of turning to prayers in their homes, hospitals and houses of worship is not. In recent years, medicine has increasingly shown an interest in investigating the effect of prayer and spirituality on health.
A survey of 31,000 adults released last year by the national Centers for Disease Control and Prevention found that 43 percent of U.S. adults prayed for their own health, while 24 percent had others pray for their health.
Some researchers say that is reason enough to study the power of prayer.
"Almost every community in the world has a prayer for the sick, which they practice when a member of their community is ill," said Dr. Mitchell Krucoff, a Duke University cardiologist and researcher in the field of distant prayer and healing. "It is a ubiquitous cultural practice, as far as we can tell. ... Cultural practices in healthcare frequently have a clue. But understanding that clue, learning how to best use it, requires basic clinical science."
WHAT STUDIES SHOW
Science has only begun to explore the power of distant healing, and the early results of this research have been inconclusive. In an article published in the Annals of Internal Medicine in 2000, researchers reported on 23 studies on various distant healing techniques, including religious, energy and spiritual healing.
Thirteen of the 23 studies indicated there are positive effects to distant healing, nine studies found no beneficial effect and one study showed a modest negative effect with the use of distant healing.
The study of distant healing was once the realm of eccentric scientists, but researchers at such prominent institutions as the Mind/Body Medical Institute in Chestnut Hill, Mass., Duke University Medical Center in North Carolina and the California Pacific Medical Center in San Francisco are involved in the field.
And the National Institutes of Health's National Center for Complementary and Alternative Medicine has spent $2.2 million on studies of distant healing and intercessory prayer since 2000 -- a small fraction of the agency's annual budget, which totaled $117 million in 2004.
Some people think even that relatively small sum of money is not being well spent.
"You can't use science to prove God," said John T. Chibnall, an associate professor of psychiatry at St. Louis University School of Medicine in Missouri, who co-wrote a scathing rebuttal of studies on distant prayer published in the Archives of Internal Medicine in 2001.
"We shouldn't waste the money of the government showing that Jesus is 'the man,' " Chibnall said in an interview. "Faith is faith. Science is science. Don't use science to strengthen or diminish belief in God."
SCIENTIFICALLY VALID?
While some scientists oppose such studies on religious or scientific grounds, others question whether it is possible to devise a scientifically valid method for measuring something as nebulous as the power of prayer.
What constitutes a "dose" of prayer? How does one define prayer? Is channeling Buddhist intention or reiki energy the same thing as praying to a Judeo-Christian God? And how do you determine whether it was prayer that made a patient better, or something else, such as the placebo effect?
"There are enormous methodological and conceptual problems with the studies of distant prayer," said Dr. Richard Sloan, a professor of behavioral medicine at Columbia University in New York. "Nothing in our understanding of our universe or ourselves suggests how the thoughts of one group of people could influence the physiology of people 3,000 miles away."
Cardiologist Randolph Byrd did the first major clinical study on distant healing at San Francisco General Hospital in 1988. He divided 393 heart patients into two groups.
One group received prayers from Christians outside the hospital; the other did not. His study, published in the Southern Medical Journal, found that the patients who were not prayed for needed more medication and were more likely to suffer complications. While it had flaws, the study garnered considerable attention.
Since then investigators have continued to look at the possible effects of remote prayer and similar distant healing techniques in the treatment of heart disease, AIDS and other illnesses as well as infertility. Numerous experiments involving prayer and distant healing have also been done involving animals and plants. One such study found that healers can increase the healing rate of wounds in mice.
"Critics often complain that if you see positive results in humans it is because of positive thinking, or the placebo response," said Dr. Larry Dossey, a retired internist in Santa Fe, N.M., and author of numerous books on spirituality and healing. "Microbes don't think positively, and are not subject to the placebo response."
In the early '90s, Elisabeth Targ and colleagues at the California Pacific Medical Center studied the effects of distant healing on 20 AIDS patients. Schlitz, who worked with Targ (who died of a brain tumor in 2002), said the study found those receiving prayer survived in greater numbers, got sick less often and recovered faster than those who did not. A follow-up study of 40 patients found similar results.
At about the same time, Duke University's Krucoff was leading a small but unusual experiment to determine if cardiac patients would recover faster after angioplasty surgery if they received any of several intangible (noetic) treatments. His study compared the results of healing touch, stress relaxation and distant healing with standard care.
Spiritual healers from around the world -- including Jews leaving prayers at the Western Wall in Jerusalem, Buddhists praying in monasteries in Nepal and France, Carmelite nuns in Baltimore offering prayers during vespers, and Moravians, Baptists and fundamental Christians praying during church -- each simultaneously prayed for one of several designated groups in the study.
All of the groups did better than the standard care group, with those receiving distant prayers doing best. He has since completed a larger, multi-site study. That study -- the largest to date -- is currently under review for publication in a medical journal.
Centerline : some results

Image 2
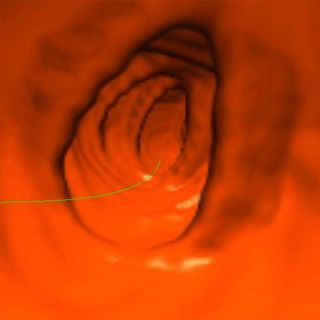
Image 3
Centerline displayed properly only when the camera is placed on a centerline point.
Change from World to Camera coordinates (-1.0 to 1.0) using the world to local transformation which also acts as the view matrix.
Change from camera to screen coordinates by multiplying by 512.0 .
Centerline not properly displayed for all points, and when camera not on centerline. Possible error in setting the projection.
Sacred Geometry
In nature, we find patterns, designs and structures from the most minuscule particles, to expressions of life discernible by human eyes, to the greater cosmos. These inevitably follow geometrical archetypes, which reveal to us the nature of each form and its vibrational resonances. They are also symbolic of the underlying metaphysical principle of the inseparable relationship of the part to the whole. It is this principle of oneness underlying all geometry that permeates the architecture of all form in its myriad diversity. This principle of interconnectedness, inseparability and union provides us with a continuous reminder of our relationship to the whole, a blueprint for the mind to the sacred foundation of all things created.
Starting with what may be the simplest and most perfect of forms, the sphere is an ultimate __expression of unity, completeness, and integrity. There is no point of view given greater or lesser importance, and all points on the surface are equally accessible and regarded by the center from which all originate. Atoms, cells, seeds, planets, and globular star systems all echo the spherical paradigm of total inclusion, acceptance, simultaneous potential and fruition, the macrocosm and microcosm.
The circle is a two-dimensional shadow of the sphere which is regarded throughout cultural history as an icon of the ineffable oneness; the indivisible fulfillment of the Universe. All other symbols and geometries reflect various aspects of the profound and consummate perfection of the circle, sphere and other higher dimensional forms of these we might imagine.
The golden ratio (a.k.a. phi ratio a.k.a. sacred cut a.k.a. golden mean a.k.a. divine proportion) is another fundamental measure that seems to crop up almost everywhere, including crops. The golden ratio is the unique ratio such that the ratio of the whole to the larger portion is the same as the ratio of the larger portion to the smaller portion. As such, it symbolically links each new generation to its ancestors, preserving the continuity of relationship as the means for retracing its lineage.
The ratio of segments in 5-pointed star (pentagram) was considered sacred to Plato & Pythagoras in their mystery schools. Note that here each larger (or smaller) section is related by the phi ratio, so that a power series of the golden ratio raised to successively higher (or lower) powers is automatically generated.
The Ancient Egyptian Pyramids and Temples were purposely built in accordance with this system.
What is Sacred Geometry?
When the teachings of geometry are used to show the ancient truth that all life emerges from the same blueprint, we can clearly see that life springs from the same source ... the intelligent force some call "God." When geometry is used to explore this great truth, a broader understanding of the universe unfolds until we can see that all aspects of reality become sacred. Understanding the simple truths of sacred geometry leads to an evolution of consciousness and an opening of the heart that is a next step in the process of human evolution.
True sacred geometric forms never fixate or stagnate on one single form. Instead they are actually in constant fluid transcendence and change (evolving or devolving) from one geometric form to another at their own speed or frequency. These ever-evolving states of geometry mirror the constantly evolving nature of the human consciousness.
Sacred Geometry in its pristine form is constructed of the fabric of conscious transcendent "Spirit Matter". These sacred geometric forms often appear in our dreams and visions. Often they are presented in a rapid-fire succession as if they were hieroglyphs with enormous amounts of emotion and meaning relayed within each symbol. In those cases, it is often not necessary to intellectually understand the meaning behind the barrage of imagery. Our
unconscious understands, and it is from there that transformation begins.
Sacred geometry and the teachings of the Flower of Life help us to see within ourselves the vastness of which we are all a part. Many humans have been conditioned to see and believe in a limited perspective of smallness. Elephant trainers of the far east tie a thin rope around the ankle of a baby elephant and throughout their lives reinforce the boundary of the rope. The adult elephant is fully capable of breaking the rope but the elephant has been so conditioned to believe he cannot, that he does not understand his own power to free himself. We are like those elephants, just learning about our self-imposed belief in limitation. Living with our limited perspectives of ourselves, we rarely see past our limitations and, as a consequence, we bind ourselves to our habits. With a little effort, the teachings of the Flower of Life and sacred geometry help us peer through the window of our conditioned beliefs and
gaze at the vastness of our true selves and our infinite potential.
Success - Subroto Bagchi
Success is defined by what you leave behind - Subroto Bagchi
The author is the vice-chairman and COO of Mind tree Consulting.
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
I was the child of a small time government servant, in a family of five brothers. My earliest memory of my father is as that of a District
Employment officer in Koraput, Orissa. It was and remains as back of the beyond as you can imagine. There was no electricity;
no primary school nearby and water did not flow out of a tap. As a result I did not go to school until the age of eight, I was home- schooled.
My father used to get transferred every year. The family belongings fitted into the back of a jeep - so the family moved form place to place
and my mother will setup an establishment without any trouble and get us going.
My parents set the foundation of my life and
the value system which makes me what I am today and largely defines what success means to me today.
As district employment officer my father was given a jeep by the government. There was no garage in the office, so the jeep was
parked in our house. My father refused to use it commute to the office. He told us that the jeep is an expensive resource given
by the government - he reiterated to us that it was not 'his jeep' but the 'government's jeep'. He also made sure that we never sat
in the government jeep - we could sit only if it is stationary. That was our early childhood lesson in governance - a lesson that
corporate managers learn the hard way, some never does.
The driver of the jeep was treated with respect due to any other member of my father's office. As small children, we were
taught not to call him by his name. We had to use the suffix 'dada' whenever we were to refer to him in public or private. When
I grew up to own a car and a driver by the name Raju was appointed I repeated the lesson to my two small daughters.
They have as a result, grown up to call Raju as 'Raju Uncle'. To me the lesson was significant -
you treat small people
with more respect than how you treat big people. It is more important to respect your subordinates than your superiors.
Our day used to start with the family huddling around my mother's chulha - an earthen fireplace she would built at each
place of posting where she would cook for the family. There was no gas, no electric stoves. The morning routine started with tea.
As the brew was served, Father would ask us to read aloud the editorial page of 'The Statesman Muffosil' edition - delivered one day by late.
We did not understand much of what we were reading. But the ritual was meant for us to know what the world was larger that
Koraput district and the English I speak today despite having studied in an Oriya medium school, has to do with that routine.
After reading the newspaper aloud we were told to fold it neatly. Father taught us a simple lesson.
He used to say "You should leave your newspaper and your toilet, the way you expect to find it".
That lesson was
about showing consideration to others. Business begins and ends that simple precept.
Being small children, we were always enamored with advertisements in the newspaper for transistor radios - we did not have one.
We saw other people having radios in their homes and each time there was an advertisement of Philips, Murphy or
bush radios we would ask our father when we could get one. Each time, my father would reply that we did not
need one because he already had five radios - alluding to his five sons. We also did not have a house of our own and
would occasionally ask father as to when like others, we would live in our own house. He would give a similar reply, "
We do not need house of our own. I already own five houses". His replies did not gladden our hearts in that instant.
Nonetheless we learnt that it is important not to measure personal success and sense of well-being through material possessions.
Government houses seldom came with fences. Mother and I collected twigs and built a small fence. After lunch, my mother would never sleep.
She would take her kitchen utensils and with those she and I would dig the rocky, white ant infested surrounding.
We planted flowering bushes. The white ants destroyed them. My mother brought ash from her chulha and mixed it in with earth and
we planted seedlings all over again. This time, they bloomed. At that time, my father's transfer order came. A few
neighbors told my mother why she is taking so much pain to beautify a government house, why she was planting seed
that would only benefit the next occupant. She said,
"I have to create bloom in a desert and whenever I am given a new place,
I must leave it more beautiful than what I had inherited." That was my first lesson in success. It is not what you create for yourself;
it is what you leave behind that defines success.
My mother began developing a cataract in her eyes when I was very small. At that time, the eldest among my brothers got a teaching
job at the University of Bhubaneswar and had to prepare for civil services examination. So it was decided that my
Mother would move to cook for him and as her appendage I had to move too. For the first time in my life, I saw electricity in
homes and water coming out of a Tap. It was around 1965 and the country was going to war with Pakistan. My mother was having
problems with reading and in any case, being Bengali, she did not know the Oriya script. So in addition to my daily chores, my job
was to read her local newspaper - end to end. That created me a sense of connectedness with a larger world. I began taking interest
in many different things. While reading out the news about the war, I felt that I was fighting the war by myself. She and I discussed the
daily news built a bond with the larger universe. In it we became part of a larger reality.
Till date, I measure my success in
terms of that sense of larger connectedness.
Meanwhile, the war raged and India was fighting on both fronts. Lal Bahadhur Shastri, the then Prime minister, coined the term
'Jai Jawan, Jai Kisan' and galvanized the nation into patriotic fervor. Other than reading out the newspaper to my mother,
I had no clue about how I could be the part of the action. So, after reading the news-paper, every day I would land up
near the university's water tank, which served the community. I would spend hours under it, imagining that there could be
spies who would come to poison the water and I have to watch for them. I would daydream about catching out one
and how the next day, I would be featured in the newspaper. Unfortunately for me, the spies at war ignored the sleepy town of
Bhubaneswar and I never got a chance to catch one in action. Yet, that act unlocked my imagination.
Imagination is everything.
If we can imagine a future, we can create it; if we can create it, others will live in it. That's the essence of success.
Over the next few years, my mother's eyesight dimmed but in me she created a larger vision, a vision with which
I continue to see the world and, I sense, through my eyes, she was seeing too. As the next few years unfolded, her vision
deteriorated and she was operated for a cataract. I remember when she turned after her operation and she saw my face
clearly for the first time, she was astonished. She said "Oh my God, I did not know you were so fair". I remain mighty pleased
with that adulation even till date. Within weeks of getting her eyesight back, she developed a corneal ulcer and, overnight,
became blind in both the eyes. That was 1969. She died in 2002. In all those 32 years of living with blindness,
she never complained about her fate even once. Curious to know what she saw with her blind eyes,
I asked her once if she sees darkness. She replied
"No, I do not see darkness. I only see light even with my eyes closed." Until she was eighty years of age, she did her morning yoga everyday, swept her own room and washed her own clothes.
To me success is about the sense of independence; it is not about seeing the world but seeing the light.
Over the many intervening years, I grew up, studied, joined the industry and began to carve my life's own journey. I
began my life as a clerk in a government office, went on to become a Management trainee with the DCM group and
eventually found my life's calling with the IT industry when fourth generation computers came to India in 1981. Life took me places -
I worked with outstanding people, challenging assignments and traveled all over the world. In 1992, while I was posted in the US,
I learnt that my Father, living a retired life with my eldest brother, had suffered a third degree burn injury and was admitted
in the Safdarjung Hospital in Delhi. I flew back to attend him - he remained for a few days in a critical stage, bandaged form neck to toe.
The Safdarjung hospital is a cockroach infested, dirty, inhuman place. The overworked, under resourced sisters in the burns ward
are both victims and perpetrators of dehumanized life at its worst. One morning while attending to my father, I realized that the
blood bottle was empty and fearing that air would go into his vein, I asked the attending nurse to change it. She bluntly told
me to do it myself. In that horrible theatre of death I was in pain and frustration and anger. Finally when she relented and came, my
Father opened his eyes and murmured to her, "Why have you not gone home yet?." Here was a man on his deathbed
but more concerned about the overworked nurse than his own state. I was stunned by his stoic self. There I learnt that
there is no limit to how concerned you can be for another human being and what the limit of inclusion is you can create.
My Father died the next day.
He was a man whose success defined by his principles, his frugality, his universalism and his sense of inclusion.
Above all he taught me that success is our ability to rise above your discomfort, whatever may be your current state.
You can, if you want, raise your consciousness above your immediate surroundings.
Success is not about building material comforts - the transistor that he never could buy or the house that he never owned.
His success was about the legacy he left, the mimetic continuity of his ideals that grew beyond the
smallness of an ill-paid, unrecognized government servant's world.
My father was a fervent believer in the British Raj. He sincerely doubted the capability of the post independence
Indian political parties to govern the country. To him, the lowering of the union jack was a sad event.
My mother was exact opposite. Consequently our house hold saw diversity in the political outlook of the two.
On major issues concerning the world the Old Man and the Old Lady had differing opinions. In them, we learnt the power of disagreements,
of dialogue and the essence of living with diversity in thinking.
Success is not about the ability to create
a definitive dogmatic end state; it is about the unfolding of thought processes, of dialogue and continuum.
Two years back, at the age of eighty-two Mother had a paralytic stroke and was lying in a government hospital in Bhubaneswar.
I flew down form the US where I was serving my second stint, to see her. I spent two weeks with her in the hospital as
she remained in a paralytic state. She was neither getting better nor moving on. Eventually I had to return to work.
While leaving her behind, I kissed her face. In that paralytic state and a garbled voice she said,
"Why are you kissing me, go kiss the world." Her river was nearing its journey, at the confluence of life and death,
this woman who came to India as a refugee, raised by a widowed mother, no more educated than High school,
married to an anonymous government servant whose last salary was Rupees three Hundred, robbed of her eyesight
by fate and crowned by adversity - was telling me to go and kiss the world!.
Success is to me about vision. It is the ability to rise above the immediacy of pain. It is about imagination.
It is about sensitivity to small people. It is about building inclusion. It is about connectedness to a larger world
existence. It is about personal tenacity. It is about giving back more to life than you take out of it.
It is about creating extraordinary success with ordinary lives.
glLines problem solved
Solved the glLines problem.
The problem was the line not being displayed for any z-value other than 0.0 because the 2d texture (itself->image->rgb) was being was being rendered above it.
Changing the value of z to 1.o from 0.0 in glVertex3f(,,) i.e. pushing the texture down to the base of the volume gave the lines for all values of z between 0.0 and 1.0
glBegin(GL_QUADS)
glTexCoord2d(0,0); glVertex3f(0,0,1);
glTexCoord2d(0,0); glVertex3f(0,512,1);
glTexCoord2d(0,0); glVertex3f(512,512,1);
glTexCoord2d(0,0); glVertex3f(512,0,0);
glEnd();
Again proceeding in the direction of drawing glLines to render the centerline.
Tried changing the color of internal 2d texture before mapping onto the widget (turned all pixels to green) and it worked. But rendering continuous centerline is certainly more complex.
So now I have to find the corresponding pixel in the 2d texture for a certain centerline position using the equations described in
volume_ray_casting(vrptrT itself, int start_x, int start_y, int width, int height, unsigned int *depth)
and the screen coordinate can be formed from the index of the rgbptr in itself->image->rgb ( lies between ([0,512],[0,512]) ) .
Then use glLines to join the points detected in that particular view.
Centerline..further development
itself->view->c_sys.origin.x,yz along with itself->x.x,y,z store the current position of the camera, and are the link which connect the camera position and the volume position being rendered.
Using this, we now come to VR.cpp which contains the method volume_ray_casting()
volume_ray_casting() is called for each frame of rendering the current 2d scene. volume_ray_casting further calls cast_ray_for_a_pixel(), WIDTH*HEIGHT times i.e. for each pixel in the 2d image to be rendered.
Before this volume_ray_casting() uses itself->view->c_sys.origin.x,y,z i.e. the current position of the camera to compute the position of the pixel and the ray direction, and passes it as an arguement to cast_ray_for_a_pixel().
cast_ray_for_a_pixel() takes in the position of the pixel as arguement and gets the appropriate color for the pixel and fills the appropriate position in image->rgb.
The above procedure gives the final 2d texture image which is mapped onto the widget.
The idea now is to use the centerline coordinates available and render the green lines appropriately. Trying to do this after the 2d texture has been mapped produces further complications as we have come out of the domain of internal coordinate systems of the colon.
So presently i think manipulating the image at the lower level, and incorporating the centerline into the 2d texture itself before it is mapped is the right way to proceed. This means i have to put the green pixels (instead of the red ones of the colon) at the correct places in image->rgb.
I have with me the position of certain points on the centerline. Traversing through the centerline points array and selecting positions around the current camera position is certainly inefficent and inaccurate.
I should be able to correspond the centerline point to the pixels being colored in cast_ray_for_a_pixel() and by locating the correct projection of the centerline point, i should override the coloring method, and color that particular pixel green and store in image->rgb.
So now we have to think about finding out whether pixel position being colored corresponds to any of the centerline point by traversing through a list. For now lets focus on just rendering those green points on the screen rather than drawing lines. Generation of a huge number of points could possibly help in viewing.
I now have to find a way to transform the centerline points to get corresponding pixel positions on the screen. Looking at how the pixel positions are got from itself->view->c_sys.origin.x,y,z might give a clue.
If this works, a future possible way of drawing continuous lines could be by using equation for a line in 3d coordinate system, and generating all the points between 2 centerline points given and coloring the appropriate pixels.
Rendering Colon Centerline
Input: Colon centerline vertices, in the global coordinate system
Output: Visible centerline in the 3d projection image for the 3D flythrough view
Procedure:
Obviously, the centerline in the 3d image projection is got by joining the visible centerline points in that part of the image with lines. (glLines)
For this the global coordinates of those points have to be converted to the local screen coordinates. The screen size - 512*512
So x - (0.0,512.0) and y - (0.0,512.0). Also z - (0.0,1.0)
So the first step should be to analyse the connection between the submarine object (camera) and 'itself' ( the object keeping track of the current 3d view). The camera coordinates are in global coordinate system ( in which the centerline vertices are) so the camera and the vertices correspond.
We have to find the corresponding screen coordinates used for rendering the image, when the camera jumps to a certain position. This transformation is the one to be applied to the vertices.
The 3d image is rendered by volume raycasting, and the resulting color values filled in the data structure is mapped as a 2d texture onto the widget.
The idea is :
* For the camera position, map into the data structure storing the centerline points, and find a certain number (?) of points, taking the point closest to the camera position as the median.
* Make these points pass through the same transformation pipeline which the camera position passes through and get the corresponding points in screen coordinates.
* The issue of lines between non-zero z values not being rendered might arise. In that case, either solve that issue or (for now), do further transformations to keep z-value 0 and get only x,y coordinates.
* If (0,512.0), gives problems, possible solution might be to use
glPushmatrix();
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(0.0,1.0,0.0,1.0,0.0,-1.0);
--Draw lines--
glMatrixMode(GL_MODELVIEW);
glPopmatrix();
* Another possible issue is the 2d image texture being drawn on the centerline.
Logically, this should give the centerline part for that portion of the image.
CAD for the Rest of us
By Andrew Madden June 29, 2005
Company: Right Hemisphere
HQ: Fremont, CA, with an R&D center in Auckland, New Zealand
Founded: 1997
Management: Michael Lynch is the chief executive officer. He was previously at 7th Level, a developer of video games. Mark Thomas is president, chief technology officer, and a co-founder of the company. He previously founded CADTech, a New Zealand-based CAD reseller. Earlier this year, Right Hemisphere appointed Robert Eve as vice president of worldwide marketing. Eve held senior level posts at several companies, including Mercury Interactive, PeopleSoft, and Oracle.
Investors: The company received Series B funding of $12.5 million from Sequoia Capital, Sutter Hill Ventures, and graphics-chip company Nvidia in April 2005.
Business Model: Right Hemisphere's software allows companies to turn their complicated engineering data and processes into displays suited for interactive training, technical documentation, and marketing communications. For instance, its product might translate an aircraft manufacturer's complex designs into visualizations and computer-generated animations. What's more, the software works with Microsoft Office, allowing 3-D files to be dropped into Word and Powerpoint files, or a PDF document using Adobe Acrobat. Right Hemisphere's target markets are the aerospace, defense, automotive, construction, and industrial equipment industries. For digital artists and graphics professionals, it also offers a free software product, Deep Paint, which enables textured painting on digital images.
Competitors: Informative Graphics, Actify, Spicer, Immersive Design, Lattice3D
Dirt: Companies such as Right Hemisphere have emerged as an adjunct to the computer aided design (CAD) software industry. Developers who work with CAD software are accustomed to its complexities, but the rest of us don't want to have to learn a new language. Thus, the aim of companies in the 3-D viewing sector is an expansionary one: to give non-technical users the ability to integrate and manipulate complex graphical data in everyday software applications.
Right Hemisphere's recent cash infusion from blue-chip investors such as Sequoia Capital and Sutter Hill Ventures is a sign of the ongoing optimism in both the company and sector -- but we're still not waiting on overnight success stories. To date, the 3-D viewing business has matured very slowly. Competitor Informative Graphics, for instance, was founded in 1990, and Spicer dates all the way back to 1983. (Did they even have software companies back then?)
A Fuzzy Image for Internet Video
Internet video once lured many smart investors into squandering their fortunes, but now many have been scared off -- and other alarm:clock news from the land of private venture funding.
nternet video has long intrigued entrepreneurs with its potential. In today's revived, post-bubble startup market, though, there's surprisingly little financial or entrepreneurial activity focused on launching new Internet video products. Sure, Microsoft, Apple, Real, and others have developed video players. And Google recently launched a Beta version of video search and the peer-to-peer video-sharing standard BitTorrent has become a cult hit. But few players can boast of winning big in the Internet video arena.
A few years ago, a number of stars from the early Internet decided to make Internet video their next stand, including the founders of Netscape and Macromedia. Their projects have been a slog, though. And we suspect they now wish they'd rested on their laurels.
We recently viewed a demo of a video portal from Netscape alumni Mike Homer and Mark Andreessen, called the Open Media Network (OMN), which is a not-for-profit outfit. Site visitors can access a free program guide to download public TV and radio programming, movies, podcasts, and video blogs, and even submit video.
While OMN seems reasonably promising, it's powered by Homer and Andreessen's for-profit, venture-backed company Kontiki, which has been slow to find its footing. Kontiki is a content management software platform developed to disseminate video as cheaply as possible. Currently, it has trials underway with the BBC and NBC.
However, Kontiki's last round of financing was an $8 million investment in December 2004, and it included just one VC firm, the Barksdale Group, which has since disbanded. Since most owners of video content have had a hard time monetizing their assets via the Internet, companies like Kontiki, which are in business to help them do so, continue to struggle.
Another struggling Internet video startup is Akimbo, which offers a TiVo-like service, delivered via a broadband Internet connection, that allows viewers to watch Internet videos on a TV. A scathing review of its TV-via-the-Internet product in the New York Times called it "a train wreck...It might just walk away with High-Tech Turkey of the Year." Despite an investment from Kleiner Perkins, whose partner William Randolph Hearst sits on Akimbo's board, Akimbo appears to be a loser, unless it can dramatically improve its value proposition.
Two Web video companies with brighter prospects are CinemaNow and iFilm. CinemaNow offers video downloads to PCs and, like Netflix, charges a subscription fee. Unlike Netflix, though, it offers popular adult films as well. CinemaNow's investors include Menlo Ventures, Microsoft, Lions Gate Entertainment, Cisco Systems, and Blockbuster.
IFilm is similar to CinemaNow, but has taken a more "guerilla" approach, serving up popular Internet video clips (think Steve Ballmer dancing), music videos, and video games, in addition to feature films. iFilm claims to have been profitable for the past couple of years. And it's backed by an impressive roster of investors, including Eastman Kodak, Sony Pictures Entertainment, Yahoo!, and Vulcan Ventures.
Courtesy:
MIT Technology Review
GPGPU: Is a Supercomputer Hiding in Your PC?
By
Chris Seitz.
Date: Jul 1, 2005.
Article Description
If you've played some of the latest, hottest video games, you've exercised your GPU in a traditional graphics sense. But other companies are now using the GPU non-traditionally, for general-purpose computation on a graphics processing unit (GPGPU). Why should you care? Because its lightning-fast, parallel computational capability makes for smooth, rich, vibrant graphics in today's games. And, repurposed, the GPU can help solve more serious problems (medical and financial) in the real world. Chris Seitz explains how.
Growth of the GPU
Were you aware that the most powerful chip in an average or better PC is not the CPU, but the GPU (graphics processing unit)? More than likely, you had an inkling that some serious technology was driving your graphics card, and over the past couple years saw the accoutrements of raw power appear: larger fans and heatsinks, and even supplementary power connectors. If you're on the bleeding edge, you may have painstakingly built a benchmark-crushing PC with a water-cooling system. The growing rage is a single PC with multiple GPUs in a scalable link interface (SLI) configuration.
Nowadays, high-performance GPUs have become more rational, with quiet thermal solutions and reasonable power requirements. But the ever-advancing video game industry entices consumers with a consistent and growing hunger for higher performance. This mass market drives a tremendous technology arms race in the GPU industry, with consumers being the overall winners. In turn, low prices for high-performance GPUs provide a great opportunity for software developers and their customers, letting them capitalize on otherwise idle transistors for their computational needs.
Perhaps management won't pay for you to use all that GPU performance during the workday, and the only exercise your powerful, computationally starved GPU gets is your lunchtime and after-work gaming sessions. That simply isn't fair to all those transistors.
So how do you convince your boss that you really need to buy the latest GPU? In fact, the argument really isn't difficult—provided that your programmers are willing and able to recast your problems to fit the massively parallel architecture of the GPU. If you can stay on the computational superhighway of the GPU, you'll be able to unleash tremendous gigaflops. Naturally, today's graphically intense applications do exactly that, using one of the two primary APIs for programming these chips: the cross-platform OpenGL API, or Microsoft's Direct3D component of the DirectX API. For example, leading games have inner loops with core algorithms that run "shaders" across an array of pixels. A shader takes in a variety of inputs—geometry and light positions, texture maps, bump maps, shadow maps, material properties, and other data—for special effects such as fog or glow. It then computes a resulting color (and possibly other data, such as transparency and depth). All this action happens for each pixel on the screen, at 60 or more frames per second—a massive amount of computation.
At its core, this processing is similar to how most computer-animated and special effects–rich movies, such as Shrek, are produced. A C-like high-level programming language is used to write shaders, and then a commercial or in-house rendering program chugs away, computing scenes on the film studio's render farm. Often comprising thousands of CPUs, these render farms handle the enormous amounts of geometry and texture data required to hit the increasing quality threshold demanded by discerning audiences of CG feature films. This rendering process is commonly done overnight, and reviews of the "dailies" (those scenes rendered overnight) are done the following morning.
GPUs go through a simplified version of this process 60 or more times per second, and each year the gap between real-time and offline rendering shrinks. In fact, many recent GPU technology demonstrations show real-time renderings of content that was generated offline just a few years ago.
Embarrassingly Parallel
Computer graphics have often been called "embarrassingly parallel." Large batches of vertices need to be transformed with identical or similar matrices. Large blocks of pixels need to be rendered with identical or similar shaders. Large images need to be blended to create a final image. Hence, the natural evolution of the GPU architecture has been toward a multithreaded single instruction multiple data (SIMD) machine with parallel execution units in three areas: the vertex, pixel, and raster portions of the chip. The architecture has also evolved to handle massive amounts of data on the GPU. Today, onboard memory is topping out at half a gigabyte, with additional fast access to main memory through PCI Express (theoretically at 4 GB/s in each direction). Internal memory bandwidth—between the GPU and its own local video memory—is around 40 GB/s.
As you can imagine, the GPU is particularly well suited to definite arenas. Certain problem sets lend themselves to the current GPU architecture, and we can confidently assume that future GPUs will become more flexible and handle previously unreasonable problem sets. In other words, the GPU is often the best tool for the job, and, due to rapid increases in brute computational power (see the trend line in Figure 1), is poised to grab more and more of the high-performance computing (HPC) market. Those experiencing the greatest performance increases have problems in which the computational or arithmetic intensity of the problem is high, meaning that many math operations occur for each piece of data that's read or written. This is because most of the transistors in GPUs are devoted to computational resources, and because memory accesses are always significantly more expensive in comparison to computation. For the same reasons, the GPU excels when off-chip communication is reduced or eliminated.
Over the past five years, the GPU has rapidly evolved into a programmable "stream processor." Conceptually, all data it processes can be considered a stream—an ordered set of data of the same datatype. Streams can range from simple arrays of integers to complex arrays of 4 × 4 32-bit floating-point matrices, or even arrays of arbitrary user-defined structures. The streams are fed through a kernel that applies the same function to each element of the entire stream. Kernels can operate on the data in multiple ways: [1]
- Transformation. Remapping.
- Expansion. Creating multiple outputs per input element.
- Reduction. Creating one output from multiple inputs.
- Filter. Outputting a subset of the input elements.
One particular restriction to flexibility is key to enabling parallel execution and high-performance computation: "[K]ernel outputs are functions only of their kernel inputs, and within a kernel." [2]
GPGPU Defined
An active community has evolved that focuses on GPGPU applications. GPGPU stands for general-purpose computation on a graphics processing unit. The web site http://www.gpgpu.org is a hub for this area, and does a fantastic job of cataloging the current and historical use of GPUs for general-purpose computation. Lately, a few seminars have covered this topic (GP2 and SIGGRAPH 2004, for example), and a full-day course at SIGGRAPH 2005 will focus on GPGPU.
If you're interested in diving right into GPGPU, read the recent book GPU Gems 2: Programming Techniques for High-Performance Graphics and General-Purpose Computation (Addison-Wesley, 2005, ISBN 0321335597), by Matt Pharr and Randima Fernando. The book focuses on the GPGPU space, devoting 14 chapters to this topic, covering everything from fundamentals to optimizations to real-world case studies. Starting by tackling the trends and underlying forces that drive streaming processing forward, plus detailing the low-level design of a modern GPU (excerpted here), the authors give readers a strong base in GPU fundamentals. Building upon that base, readers learn more thoroughly the detailed differences between the CPU and GPU, strengths and weaknesses of each, and how to most efficiently map computational concepts to the various portions of the GPU. Efficiently harnessing the GPU for computation is then discussed, with focus on parallel data structures, flow-control idioms, and program optimization.
GPGPU in the Real World
Most of GPU Gems 2 is structured in a "gem"-style fashion, detailing best practices and cutting-edge uses of the GPU—particularly advanced graphics techniques. But the book also provides numerous examples of how GPUs have excelled at GPGPU tasks.
A particularly interesting chapter (and perhaps profitable to certain readers) discusses computational finance and the pricing of options. GPUs are demonstrated to be far superior to CPUs for the task of efficiently determining the fair value of options (in this case, tens of thousands of options simultaneously). This task concerns Wall Street institutions intimately, in part due to a need to hold sufficiently large cash reserves to cover market fluctuations. Because this requirement necessitates borrowing large sums at overnight interest rates, accurate, timely calculations lead to less conservative, more accurate borrowing, and therefore less interest paid. This example from the world of financial engineering shows how GPUs can be extremely useful for decidedly non-graphical problems. Other examples touch on computational biology (protein structure prediction), partial differential equations (such as those used in physics simulation), sorting algorithms, fluid flow (the Lattice Boltzmann Method), and fast Fourier Transforms (FFTs) on the GPU.
The International Technology Roadmap for Semiconductors (ITRS) compiles the industry trends and has forecast a 71% increase in capability of chips year after year. [3] That incredible growth rate, compounded with the ability to build configurations with multiple GPUs operating in parallel via SLI, makes it likely that the GPU will continue to subsume functionality (previously belonging to CPUs) for increasingly mainstream computation. Chances are that opportunities exist in your own business for GPGPU computation. It's well worth exploring this field and jumping on the train soon, because it's only getting faster as GPUs increase in performance, functionality, and programmability.
References
[1] GPU Gems 2, Chapter 29.
[2] GPU Gems 2, p. 465.
[3] GPU Gems 2, p. 458.
Courtesy: Informit


